Wie können Sie die Messunsicherheit berechnen, wenn Ihnen keine Referenzprobe vorliegt?

Die international anerkannte Methode zur Berechnung der Messunsicherheit – GUM – setzt das Vorhandensein einer zertifizierten Referenzprobe voraus. Darüber hinaus werden Referenzproben dazu verwendet, die gleichbleibende Abweichung Ihres Analysegerätes (d.h. die systematische Abweichung des Mittelwertes) zu bestimmen.

Doch was tun, wenn man keine Referenzprobe zur Hand hat? Oder wenn sich die vorhandenen Referenzproben nicht auf den interessierenden Bereich beziehen? In diesen Fällen können Ihnen verschiedene statistische Methoden weiterhelfen. Bevor wir uns näher mit diesen Methoden beschäftigen, müssen wir noch klären, was genau wir unter Messunsicherheit verstehen.

Die Messunsicherheit wird von der Richtigkeit und Präzision bestimmt

Wie bereits in einem früheren Post zum Thema Messunsicherheit erklärt, hängt eine genaue Messung von zwei Kriterien ab:

Die Genauigkeit des Mittelwertes (Richtigkeit). Hiermit wird ausgedrückt, wie weit der Mittelwert unserer Messungen von dem Erwartungswert abweicht. Diese Art von Messfehlern äußert sich in Form einer systematischen Abweichung vom Mittelwert, und zwar bei jeder Messung, die wir mit unserem Messgerät vornehmen.

Die Präzision. Wird die gleiche Messung mehrere Male durchführen, dann ist die Präzision ein Maß dafür, wie dicht die Messergebnisse beieinander liegen. Eine geringe Präzision bedeutet, dass es zwischen den einzelnen Messungen große Abweichungen gibt; eine hohe Präzision bedeutet dagegen, dass die Messwerte dicht beieinander liegen. Die Präzision ist von zufälligen Abweichungen abhängig. Somit unterliegen die Messwerte einer Normalverteilung.

Um ein verlässliches Vertrauensintervall für die Genauigkeit zu erhalten, müssen wir beides - die Richtigkeit und die Präzision - berechnen und die jeweiligen Ergebnisse zusammenführen.

Berechnung der Genauigkeit des Mittelwertes ohne Referenzprobe

In Fällen, in denen uns eine Referenzprobe mit einer bekannten Zusammensetzung vorliegt, können wird den zertifizierten Wert einfach mit unseren eigenen gemittelten Messwerten vergleichen und die festgestellte Abweichung auf alle unsere Messergebnisse anwenden. Wenn diese Möglichkeit nicht besteht, müssen wir auf eine andere Methode zurückgreifen, und zwar auf die Methode des Standard Error of the Estimate (SEE).

Für die Berechnung des SEE wird folgende Gleichung verwendet:

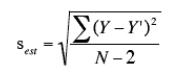
Mit:

sest: Standard Error of the Estimate

Y: Tatsächlicher vom Messgerät gemessener Wert

Y’: Ergebnis der Regressionsanalyse

N: Anzahl der Werte

Lassen Sie uns das Ganze anhand von konkreten Werten veranschaulichen. Nehmen wir die folgenden von einem Spektrometer während der Kalibration ermittelten Messwerte.

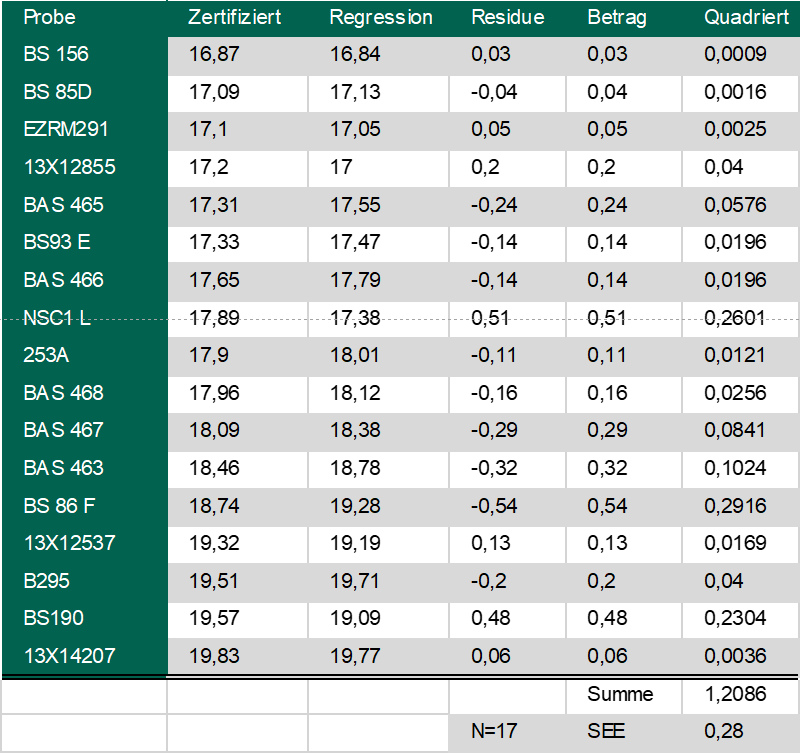
In der ersten Spalte der Tabelle stehen die gemessenen Werte, in der zweiten die mit Hilfe einer Software ermittelten Werte aus der Regressionsanalyse. Setzen wir diese Werte in die genannte Gleichung ein, dann erhalten wir eine SEE-Abweichung von 0,28 %.
Man erkennt die Ähnlichkeit zur Berechnung der Standardabweichung, sodass man sich den SEE ebenfalls als statistische Verteilung der Abweichungen der Regressionswerte in Bezug auf die Erwartungswerte (zertifizierten Werte) vorstellen kann.

Berechnung der Präzision ohne Referenzprobe

In den Fällen, in denen wir das GUM-Verfahren zur Berechnung der Messungenauigkeit aufgrund von zufälligen Abweichungen nicht anwenden können, greifen wir auf die sogenannte Student-t-Verteilung to previous post on this topic> zurück. Diese Verteilungsfunktion wurde für Fälle entwickelt, bei denen nur eine geringe Anzahl von Proben vorliegt.

Nach der Student-t-Verteilungsfunktion wird das Vertrauensintervall ausgedrückt mit:

uc= x̅ +/- Tx

Mit:

x̅: Durchschnitt der gemessenen Werte

TX: Wert der t-Verteilungsfunktion. Dieser Wert wird mit der folgenden Formel berechnet:

Tx= (t (f,P) x s / N1/2

Mit:

t: Tabellarischer Wert, abhängig von f (Anzahl der Freiheitsgrade) und P (der gewünschten statistischen Sicherheit).

s: Standardabweichung der Messreihe

N: Anzahl der durchgeführten Analysen

Nehmen wir an, dass wir eine unbekannte Probe 10 Mal gemessen haben und die folgenden Werte für den Chromanteil erhalten haben:

Der durchschnittliche Chromgehalt nach 10 Messungen: 18.82%
Standardabweichung 0,15%

Wir nehmen an, dass unsere Vertrauenswahrscheinlichkeit bei 95 % liegen soll. Nach Eingabe der entsprechenden Werte in die Gleichung ergibt sich:

n: 10
P: 95%
s: 0,15%
t: 2,262 (bei P: 95 % und 10)

Daraus ergibt sich ein Vertrauensintervall von:
Uc = +/-0·11%

Wie bringen wir Richtigkeit und Präzision zusammen?

Nun liegen uns alle Voraussetzungen vor, um die gesamte Messunsicherheit zu berechnen. Unser Endergebnis erhalten wir, indem wir unseren Wert +/- 0,11 % für die Präzision und den Wert +/-0,28 % für die Genauigkeit des Mittelwertes addieren:

C = 18,82 % +/- 0,39% bei einer Wahrscheinlichkeit von 95 %.

Wir möchten darauf hinweisen, dass dieser Weg zur Beschreibung eines Gesamtfehlers nur einer von vielen ist. Es hängt stark von der Methode, den verfügbaren Daten und der geforderten Sicherheit ab, welche Annahme die geeignetere ist. Wir möchten eine Möglichkeit aufzeigen, die zu mindestens schlüssig aus einfach verfügbaren Messwerten eine Abschätzung erlaubt.

Sind Sie an weitergehenden Informationen interessiert?

In unserem Leitfaden „Die Suche nach den wahren Werten: So können Sie die Genauigkeit von analytischen Messungen abschätzen und deren Abweichung berechnen“ gehen wir noch näher auf diese Berechnungsmethode ein. Nach einer Einführung in die Grundlagen der Statistik erläutern wir in diesem Leitfaden unterschiedliche Methoden, mit denen Sie die Messunsicherheit der von Ihnen durchgeführten Materialanalysen berechnen können. Registrieren Sie sich noch heute unter diesem Link, um unseren Leitfaden zu downloaden.

Diesen Blog teilen