Qualitätssicherung / -kontrolle
Metallproduktion / Gießereien
Sicherheitsprüfung (PMI)
Schrottsortierung / Recycling
Maschinenbau
Metallveredelung / -galvanisierung / beschichtung
Elektronik
Zu den aussagekräftigsten Methoden zur Berechnung der Messunsicherheit zählt das sogenannte GUM-Verfahren, ein von der ISO (International Organisation for Standardisation) und dem BIPM (Bureau International des Poids et Mesures) empfohlenes Verfahren. GUM steht für „Guide to the Expression of Uncertainty in Measurement“.
Dieses Verfahren kann angewendet werden, wenn Ihnen eine zertifizierte Referenzprobe vorliegt, die eine ähnliche Zusammensetzung aufweist wie die zu erwartende Zusammensetzung Ihrer unbekannten Probe aus der Produktion. Das Verfahren ist deshalb so aussagekräftig, weil es alle Abweichungen aus allen für ein möglichst genaues Messergebnis durchgeführten Messungen berücksichtigt. Das heißt, in die Berechnung fließen die Abweichung des Zertifikatswertes der Referenzprobe, die Abweichung Ihrer eigenen Messungen der Referenzprobe und die Abweichung Ihrer Messungen der unbekannten Probe ein.
Die Gleichung zur Berechnung des Vertrauensbereichs nach GUM lautet wie folgt:
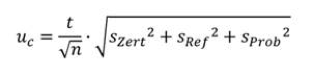
Bevor wir die Berechnung an einem Beispiel durchführen, möchten wir kurz die einzelnen Glieder der Gleichung erklären.
t = der Wert der Student-t-Verteilungsfunktion. Hierbei handelt es sich um einen Multiplikationsfaktor, der bei statistischen Systemen, bei denen es eine vergleichsweise geringe Anzahl von Messungen (Werten) gibt, verwendet wird. Der Wert t ist von zwei Faktoren abhängig: der Anzahl der Messungen und dem gewünschten Vertrauensintervall. Die Werte für t können entsprechenden frei zugänglichen Tabellen entnommen werden.
n = die Anzahl der von Ihnen durchgeführten Messungen der Referenzprobe und der unbekannten Probe. Die Anzahl der Messungen sollten für alle Proben gleich sein!
szert = die Standardabweichung des Zertifikatswertes der Referenzprobe. Wird aus dem mit der Referenzprobe gelieferten Zertifikat entnommen.
sref = die Standardabweichung unserer Messungen der Referenzprobe.
sprob = die Standardabweichung unserer Messungen der unbekannten Probe.
Für die Berechnung der Messungenauigkeit muss zunächst ein Vertrauensintervall festgelegt werden. In unserer Beispielrechnung verwenden wir 95%, ein für Materialanalysen üblicher Wert.
Für den Chromgehalt der Probe nehmen wir folgende Werte an:
| Cr | |
| Durchschnittswert der Referenzprobe entsprechend dem Zertifikat | 18.46% |
| Standardabweichung der Referenzprobe entsprechend dem Zertifikat, szert | 0.05% |
| Durchschnittswert aus der Analyse (10 Messungen) der Referenzprobe | 18.54% |
| Standardabweichung aus der Analyse der Referenzprobe, sref | 0.1% |
| Durchschnittswert aus der Analyse (10 Messungen) der unbekannten Probe | 18.82% |
| Standardabweichung der Analyse der unbekannten Probe, sprob | 0.15% |
t: 2,262 für ein Vertrauensintervall von 95% und 10 Proben (f=n-1)
n: 10 (10 Messungen pro Probe)
Eingesetzt in die Gleichung erhalten wir:
Uc = 0,134%.
Dies bedeutet: Wir können zu 95% sicher sein, dass unsere unbekannte Probe einen Chromanteil von 18,82% +/- 0,13% gemäß GUM-Berechnung enthält.
Allerdings haben wir bis hierher nur die zufälligen Abweichungen vom Mittelwert berücksichtigt, nicht die mögliche systematische Abweichung vom Mittelwert. Um die gesamte Messungenauigkeit bestimmen zu können, muss zusätzlich die Genauigkeit des Mittels (bzw. die Richtigkeit) in die Berechnungen einfließen. So kann in diesem Fall die gemessene Konzentration der unbekannten Probe um 0,08% nach unten korrigiert werden, womit die systematische Abweichung zwischen der zertifizierten Probe und der Messung dieser Probe auf dem Gerät selbst korrigiert wird. Oft ermöglicht die Gerätesoftware diesen Schritt automatisch auszuführen, die sogenannte ‚Typ-Rekalibration‘.
In unserem umfassenden Leitfaden „Die Suche nach den wahren Werten: Berechnung der Messungenauigkeit bei Materialanalysen“ erfahren Sie, wie Sie in der Praxis die Abweichungen Ihrer analytischen Messungen selbst berechnen können, warum Fehler überhaupt entstehen und was Sie tun können, wenn Ihnen keine Referenzprobe vorliegt. Registrieren Sie sich noch heute unter diesem Link, um unseren Leitfaden zu downloaden.

Thermische Charakterisierung von Materialien für Batterien in Forschung und Entwicklung
Mehr erfahren