Einführung in die Statistik für Messungen mit Funkenspektrometer

Wenn wir eine Messung mit Funkenspektrometer vornehmen, erwarten wir, dass das Ergebnis genau und präzise ist. Wie genau und präzise jedoch das Ergebnis in Wahrheit ist, hängt von zahlreichen Faktoren ab. Fakt ist, dass in der Praxis jede Messung fehlerbehaftet ist. Tatsächlich sind die Ergebnisse aus einer spektroskopischen Messung erst dann vollständig, wenn wir die Abweichung berücksichtigten, z.B. die gemessene Konzentration hat einen Mittelwert 20 % mit einer möglichen Abweichung von +/- 0,2%.

Die Abweichung wird u.a. von zufälligen Fehlern im Messsystem bestimmt. Sie unterliegt dabei statistischen Regeln. Diese Regeln zu verstehen und richtig anzuwenden ist der erste Schritt auf dem Weg, die Abweichung der eigenen Messungen richtig einschätzen zu können.

Wie sind zufällige Fehler verteilt?

Alle Werte einer einzelnen Variablen einer Grundgesamtheit liegen innerhalb der sogenannten Normalverteilung oder Gauß’schen Glockenkurve.

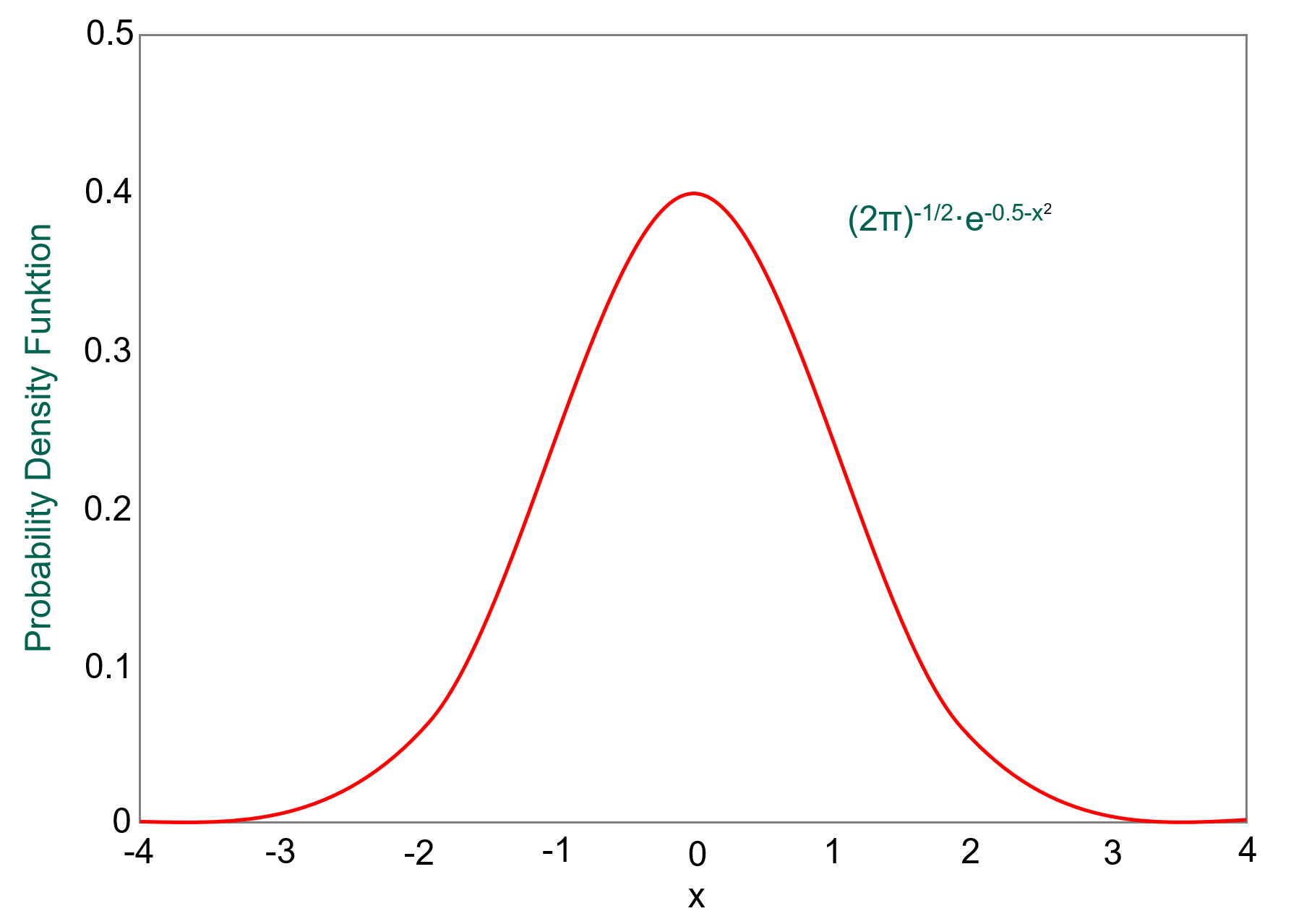
Betrachten wir als Beispiel die Variable 'Größe'. Nehmen wir an, dass wir die Größe aller Frauen gemessen haben und die Ergebnisse in einem Koordinatensystem graphisch darstellen: Die Größenangaben werden auf der y-Achse und die Anzahl der Frauen mit den jeweiligen Größen auf der x-Achse aufgetragen. Die Kurve hätte den Verlauf der oben dargestellten Normalverteilung: Die Mehrheit der Personen, d.h. diejenigen mit durchschnittlichen Größen, würden den mittleren Bereich abdecken. Gleichzeitig würde die Kurve jeweils nach rechts und links auslaufen - hin zu den zunehmend kleineren bzw. größeren Frauen.

Was versteht man unter Standardabweichung?

Ein Blick auf den Kurvenverlauf zeigt: je breiter die Normalverteilung, desto mehr Werte befinden sich in einem größeren Abstand zum Mittelwert, bzw. je schmaler die Normalverteilung, desto mehr Werte befinden sich in der Nähe des Mittelwertes. Die Standardabweichung σ ist ein numerischer Wert, der angibt, innerhalb welcher Streubreite die Messergebnisse liegen.

Bei der Normalverteilung gilt immer:

68,25% der Messwerte haben eine Abweichung von höchstens 1σ vom Mittelwert.
95,45% der Messwerte haben eine Abweichung von höchstens 2σ vom Mittelwert.
99,73% der Messwerte haben eine Abweichung von höchstens 3σ vom Mittelwert.

Für spektroskopische Messungen gilt: je kleiner der Wert der Standardabweichung und je schmaler die Kurve der Normalverteilung, desto präziser sind unsere Messungen. Die Standardabweichung σ lässt sich mit der folgenden Formel berechnen:

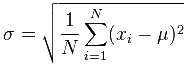
Mit:
μ: Mittelwert der Grundgesamtheit
xi: Messwerte
N: Anzahl der Messwerte

Anwendung in der Praxis

In der Praxis messen wir in der Regel nicht die komplette Grundgesamtheit, sondern nur Stichproben.

Bei spektroskopischen Messungen ist die Zahl der gemessenen Proben normalerweise nicht groß genug, um für die komplette Grundgesamtheit die Standardabweichung σ genau berechnen zu können. Wir messen hier nur eine Stichprobe. Glücklicherweise gibt es eine leicht abgewandelte Formel, mit der man in diesem Fall die Standardabweichung der Stichprobe abschätzen kann. Mit dem Symbol s wird zum Ausdruck gebracht, dass es sich um die Standardabweichung einer Stichprobe handelt.
s ergibt sich aus:

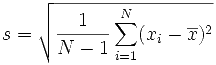
Mit:
x̅: Mittelwert aller Messwerte
xi: Messwerte
N: Anzahl der Messwerte

Mit dieser Standardabweichung (s) der Stichprobe kann man die Abweichung unserer spektroskopischen Messungen abschätzen. Wenn wir sicher gehen wollen, dass ca. 95 % unserer Messwerte innerhalb der vorgegebenen Toleranzen liegen, ergibt sich – angesichts der genannten Regel, dass bei einer Normalverteilung 95,45 % aller Messwerte eine Abweichung von höchstens 2s haben – , folgende Gleichung:

Konzentration=<Durchschnittswert aller Messungen>% +/- 2 x s%

Dies bedeutet zum Beispiel: Um sicher sein zu können, dass unsere gemessene Konzentration innerhalb einer Toleranz von 20% +/- 0.2 liegt, muss s gleich 0,1 sein.

Jedoch ist diese Genauigkeit für die Spektroskopie in der Regel noch nicht ausreichend. Vielmehr muss noch eine weitere Variable berücksichtigt werden, mit der wir uns im nächsten Blog beschäftigen wollen.

Sind Sie an weitergehenden Informationen interessiert?

Ab sofort steht Ihnen unser Leitfaden „Die Suche nach den wahren Werten“, der sich mit den Grundlagen der Statistik befasst, zur Verfügung. In diesem Leitfaden zeigen wir anhand von konkreten spektroskopischen Messungen, wie Sie die wahre Abweichung Ihrer Messungen auch dann abschätzen können, wenn Ihnen bestimmte Informationen nicht vorliegen. Registrieren Sie sich noch heute unter diesem Link, um unseren Leitfaden zu downloaden.

Diesen Blog teilen